ベルトランのパラドクス(ベルトランの逆説)というものがあります。超簡潔に言えば「ランダム」ってなんだ?という「確率の定義」に関する話です。今回はJavascriptでシミュレータを作りました。
ベルトランのパラドックスとは
とある円とそれに内接する正三角形がある。この円のランダムに弦を引いたとき、弦が正三角形の1辺よりも、長くなる確率はいくらか。
という問題がベルトランのパラドクス(ベルトランの逆説 / Bertrand paradox)です。
結論から言うと、答えは3つあり、「ランダムな弦の引き方」によって、1/2、1/3、1/4、というものです。
一体どの答えが正解なのか・・・ということです。
3つの答えについて
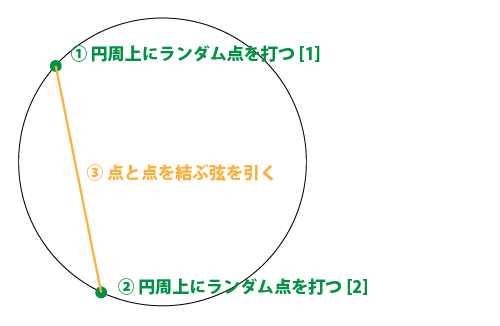
case:1 (答えが1/3になる考え方)
円周上に、ランダムに位置する2点を定め、弦を引く場合。この場合に答えが1/3になる。
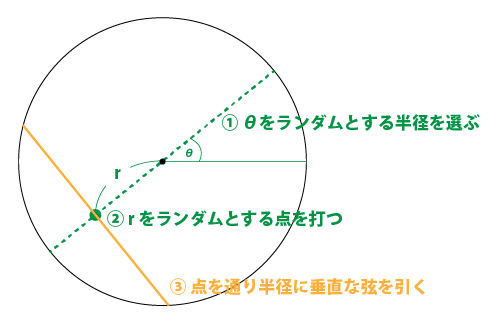
case:2 (答えが1/2になる考え方)
The “random radial point” method:
円の半径をランダムに選んで、その半径上にランダムで点(つまり極座標でいうところの、rとθがランダム)を定め、その点を通り、半径に垂直な弦を引く場合。この場合に答えが1/2になる。
case:3 (答えが1/4になる考え方)
The “random midpoint” method:
円の内部にランダムに点を定め、その点が中点となるような弦を引く場合。この場合に答えが1/4になる。
理論的になぜそうなるのか
理論的な計算方法やその解説はベルトランの逆説 – Wikipedia等のわかりやすいサイトでご確認ください!
実際にそうなるのか
Javacriptシミュレーター
というわけで、実際に上記3パターンでプログラムを組んだ場合に、本当にそのとおりの確率になるのか調べるためにプログラムをJavascriptで作りました。
https://1-10000th.com/bertrand_paradox/
使い方・仕様
ランダムな弦の数、アニメーション速度、弦の太さ、弦の中点の点の半径、各種カラーを設定して、スタートを押します。スマホにも対応しています。
著作権とか
授業とかで自由に使っていただいて結構です(ただし、デバッグはあまりしていません)。コメントいただけると私が喜びます。
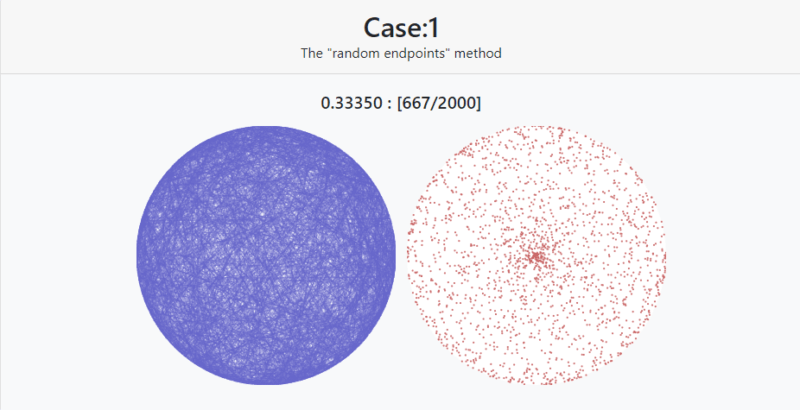
結果 | Case1: The “random endpoints” method
弦を2000本Case1の方法でランダムに引いた結果です。0.33350という数字が確率です。
左の円が弦を表示、右の円が弦の中点をプロットしたものです。
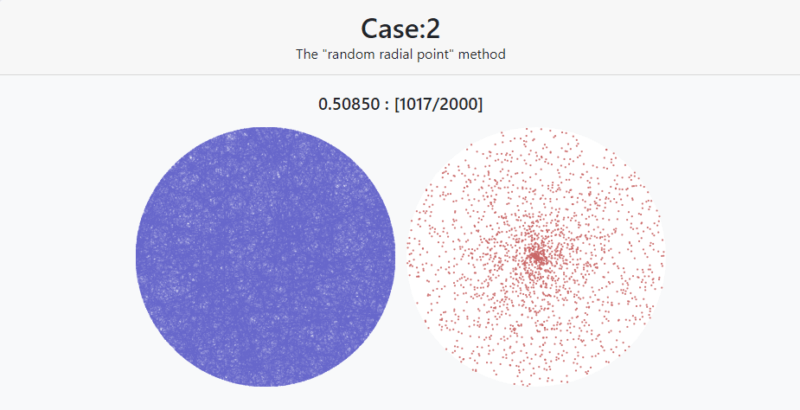
結果 | Case2: The “random radial point” method
弦を2000本Case2の方法でランダムに引いた結果です。0.50850という数字が確率です。
左の円が弦を表示、右の円が弦の中点をプロットしたものです。
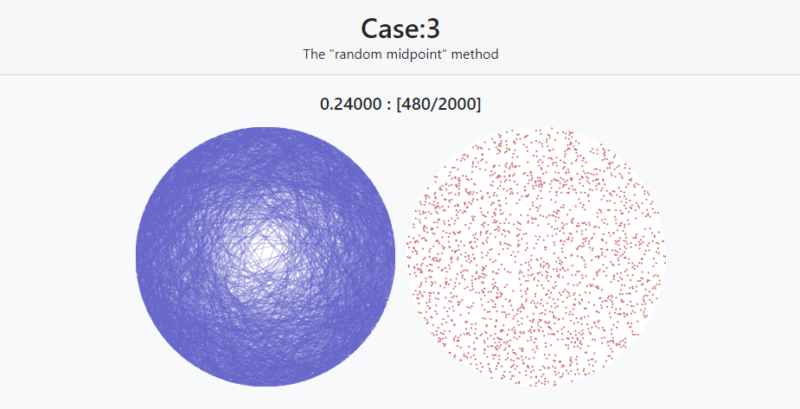
結果 | Case3: The “random midpoint” method
弦を2000本Case3の方法でランダムに引いた結果です。0.24000という数字が確率です。
左の円が弦を表示、右の円が弦の中点をプロットしたものです。
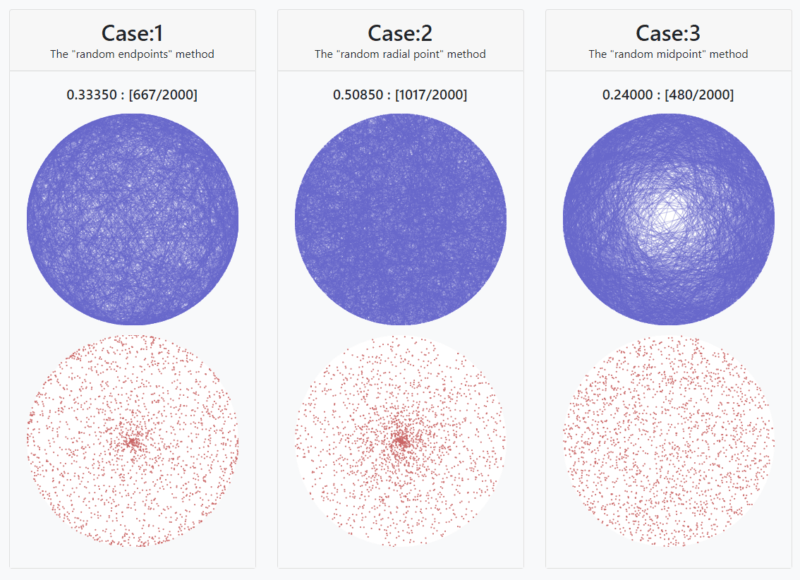
結果の比較
全部一気に表示すると上記になりました。
学問的な考察は省略しますが、図に注目してもらうと、円に「ランダムに弦を引く」という目的に対し、それぞれ偏りがあることがあることがわかると思います。
ぜひ、シミュレータページで試してください。
まとめ
ものすごく大雑把に言うと、「ランダムに弦を引く」という問題は、実は問題として曖昧(学問的に言うと「確率空間の定義が曖昧」)で、場合によっては確率は変わってしまいますよ。ですから確率を見るときは、場合によってはちゃんと条件(確率空間)を確認してね!ということです。おそらく!
Javascriptのソースコードの説明はまた機会があったら。