Javascriptによる円と直線の交点の座標の計算（ベクトルの知識必要なしver）

中学生で習う範囲で、ベクトルを使わずに、円と直線の交点を算出するプログラムを書いてみます。

目的

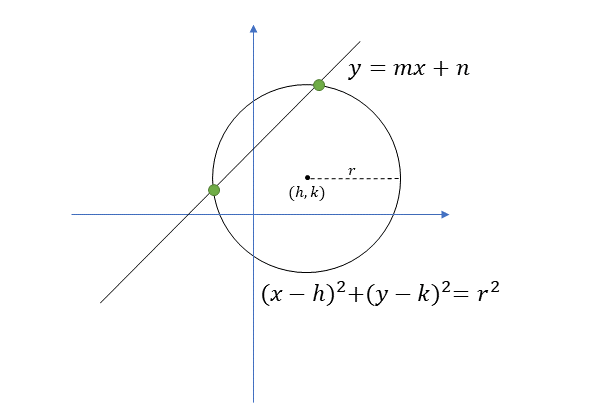
円の中心座標 $(h,k)$ と半径 $r$ と直線の式 $y=mx+n$ が与えられている時、円と直線の交点（上記図の緑の点の座標）を求めたいと思います。

アルゴリズム

円の方程式は下記の通りとする。

$$(x-h)^{2}+(y-k)^{2}=r^{2}$$

直線の方程式は下記の通りとする。

$$y=mx+n$$

ここで、直線の式の $y$ を円の方程式に代入すると下記になり、

$$(x-h)^{2}+(mx+n-k)^{2}=r^{2}$$

カッコを展開すると下記になる。

$$x^{2}-2xh+h^{2}+m^{2}x^{2}+2mx(n-k)+(n-k)^{2}=r^{2}$$

この式を形を解の公式： $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ が使えるように、適当にカッコでくくり、 $r^{2}$ を左に持ってくると下記になる。

$$(1+m^{2})x^{2}+(-2h+2m(n-k))x+h^{2}+(n-k)^{2}-r^{2}=0$$

ここで下記のとおりにする。

$a=1+m^{2}$

$b=-2h+2m(n-k)$

$c=h^{2}+(n-k)^{2}-r^{2}$

上記を使うと、上記の式は下記になる。

$$ax^{2}+bx+c=0$$

よって、解の公式から答え $x$ が導き出せる。

$x$ が出れば $y=mx+n$ に代入して $y$ がでる。

なお、下記のように置くと

$$D=b^{2}-4ac$$

$D$ の値によって、下記のように答えが分かれる。

$D>0$ の場合は答えが2つでる（つまり2点で交わる）。

$D=0$ の場合は答えが1つでる（つまり1点で交わる。直線が円の接線となる）。

$D>0$ の場合は答えが2つでる（交わらない）。

以上。

プログラム（javascript）

これをJavascriptで記述すると下記のとおりになる（交点座標を返す関数）。

//////////////////////////////
// 円の方程式は (x - h)^2 + (y - k)^2 = r^2
// 線の方程式は y = m * x + n
// r: 円の半径
// h: 円の中心のx座標
// k: 円の中心のy座標
// m: 直線の傾き
// n: 直線の切片
//////////////////////////////
function kouten(r, h, k, m, n) {
  var a = 1 + Math.pow(m, 2);
  var b = -2 * h + 2 * m * (n - k);
  var c = Math.pow(h, 2) + Math.pow((n - k), 2) - Math.pow(r, 2);
  var D = Math.pow(b, 2) - 4 * a * c;

  var kouten = [];
  if (D >= 0) {
    var x1 = (-b + Math.sqrt(Math.pow(b, 2) - 4 * a * c)) / (2 * a);
    var x2 = (-b - Math.sqrt(Math.pow(b, 2) - 4 * a * c)) / (2 * a);
    if (D == 0) {
      //Dがゼロなら、1点だけが答え
      kouten.push({ x: x1, y: m * x1 + n});
    } else {
      //Dがゼロより上なら、2点が答え
      kouten.push({ x: x1, y: m * x1 + n});
      kouten.push({ x: x2, y: m * x2 + n});
    }
  }
  return kouten;
}

実行結果（jsfiddle）

適当にボタンを何回かクリックしてください。ランダムで円と直線が現れて、交差していれば、赤い文字で交点の座標が表示されます。